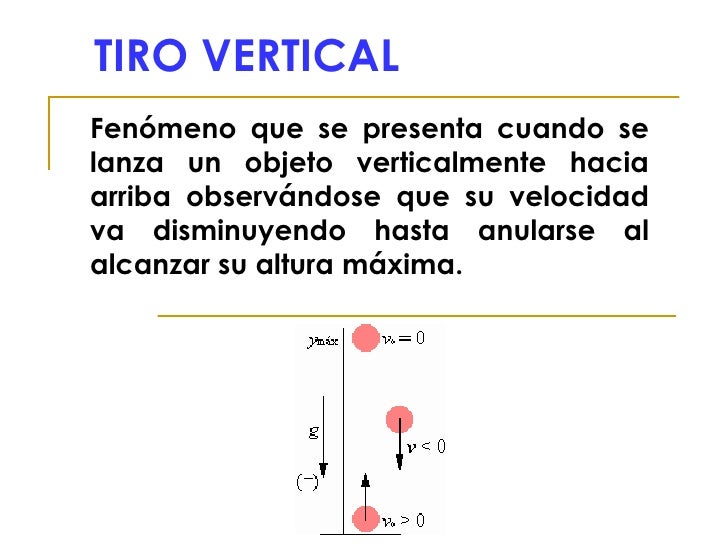
TIRO VERTICAL

FÓRMULAS

EJERCICIOS

EJERCICIOS

Problema n° 1) Se lanza un cuerpo verticalmente hacia abajo con una velocidad inicial de 7 m/s.

a) ¿Cuál será su velocidad luego de haber descendido 3 s?.

b) ¿Qué distancia habrá descendido en esos 3 s?.

c) ¿Cuál será su velocidad después de haber descendido 14 m?.

d) Si el cuerpo se lanzó desde una altura de 200 m, ¿en cuánto tiempo alcanzará el suelo?.

e) ¿Con qué velocidad lo hará?.

Usar g = 10 m/s².

Desarrollo

Datos:

v₀ = 7 m/s

t = 3 s

y = 200 m

h = 14 m

Ecuaciones:

(1) v_f = v₀ + g.t

(2) y = v₀.t + g.t²/2

(3) v_f² - v₀² = 2.g.h

a) De la ecuación (1):

v_f = (7 m/s) + (10 m/s²).(3 s)
v_f = 37 m/s

b) De la ecuación (2):

Δh = (7 m/s).(3 s) + (10 m/s²).(3 s)²/2
Δ h = 66 m

c) De la ecuación (3):

v_f = √v₀² + 2.g.h

v_f = 18,14 m/s

d) De la ecuación (2):

0 = v₀.t + g.t²/2 - y

Aplicamos la ecuación cuadrática que dará dos resultados:

t₁ = 5,66 s

t₂ = -7,06 s (NO ES SOLUCION)

e) De la ecuación (3):

v_f = √v₀² + 2.g.h

v_f = 63,63 m/s

Problema n° 2) Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial de 100 m/s, luego de 4 s de efectuado el lanzamiento su velocidad es de 60 m/s.

a) ¿Cuál es la altura máxima alcanzada?.

b) ¿En qué tiempo recorre el móvil esa distancia?.

c) ¿Cuánto tarda en volver al punto de partida desde que se lo lanzo?.

d) ¿Cuánto tarda en alcanzar alturas de 300 m y 600 m?.

Usar g = 10 m/s².

Desarrollo

Datos:

v₀ = 100 m/s

v_f = 60 m/s

t = 4 s

y₁ = 300 m

y₂ = 600 m

Ecuaciones:

(1) v_f = v₀ + g.t

(2) y = v₀.t + g.t²/2

(3) v_f² - v₀² = 2.g.h

a) Para la altura máxima v_f = 0, de la ecuación (3):

-v₀² = 2.g.h
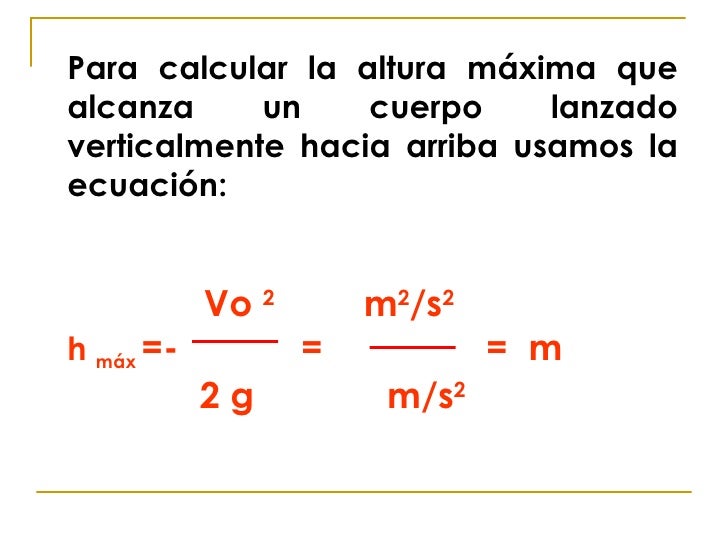
h _máx = -v_f²/(2.g)⇒ h _máx = -(100 m/s)²/[2.(-10 m/s²)]

h _máx = 500 m

b) De la ecuación (1) y para v_f = 0:

t = v₀/g

t = (-100 m/s)/(-10 m/s²)

t = 10 s

c) Recordemos que en tiro vertical, cuando un objeto es lanzado hacia arriba y luego cae, cuando vuelve a pasar por el punto de partida posee la misma velocidad que en el momento del lanzamiento pero con sentido contrario (v_f = -v₀).

Podemos asegurar que el resultado pedido es el doble del tiempo que requirió para alcanzar la altura máxima.

t = 20 s

e) No puede alcanzar una altura de 600 m porque la máxima es de 500 m. Para h = 300 m empleamos la ecuación (2):

0 = v₀.t + g.t²/2 - y

Aplicamos la ecuación cuadrática (Báscara) que dará dos resultados:

t₁ = 3,67 s

t₂ = 16,32 s (NO ES SOLUCION)

Problema n° 3) Un observador situado a 40 m de altura ve pasar un cuerpo hacia arriba con una cierta velocidad y al cabo de 10 s lo ve pasar hacia abajo, con una velocidad igual en módulo pero de distinto sentido.

a) ¿Cuál fue la velocidad inicial del móvil?.

b) ¿Cuál fue la altura máxima alcanzada?.

Usar g = 10 m/s².

Desarrollo

Datos:

t = 10 s

y = 40 m

Ecuaciones:

(1) v_f = v₀ + g.t

(2) y = y₀ + v₀.t + g.t²/2

(3) v_f² - v₀² = 2.g.h

a) Los 10 s se componen de 5 s hasta alcanzar la altura máxima (v_f = 0) y 5 s para regresar, de la ecuación (1):

0 = v₀ + g.t
v₀ = -g.t
v₀ = -(-10 m/s²).(5 s)
v₀ = 50 m/s (a nivel del observador).

Esta velocidad inicial la tomaremos como la final usando la fórmula (3):

v_f² - v₀² = 2.g.h

(50 m/s)² - v₀² = 2.(-10 m/s²).(40 m)

(50 m/s)² - 2.(-10 m/s²).(40 m) = v₀²

v₀ = 57,45 m/s (a nivel de lanzamiento)

b) Nuevamente con la ecuación (3) calculamos la distancia recorrida desde el observador hasta la altura final:

v_f² - v₀² = 2.g.h

(0 m/s)² - (50 m/s)² = 2.(-10 m/s²).h

h = 125 m

Finalmente sumamos la altura máxima y la altura del observador:

h = 125 m + 40 m

h = 165 m

Tiro vertical. TP-11

Cinemática: Solución del ejercicio n° 4

Problema n° 4) Desde un 5° piso de un edificio se arroja una piedra verticalmente hacia arriba con una velocidad de 90 km/h, ¿cuánto tardará en llegar a la altura máxima?.

Usar g = 10 m/s².

Desarrollo

Datos:

v₀ = 90 km/h
v₀ = 25 m/s

Ecuaciones:

(1) v_f = v₀ + g.t

(2) y = v₀.t + g.t²/2

(3) v_f² - v₀² = 2.g.h

Para v_f = 0 empleamos la ecuación (1):

0 = v₀ + g.t
t = -v₀/g
t = -(25 m/s).(-10 m/s²)
t = 2,5 s

Tiro vertical. TP-11

Cinemática: Solución del ejercicio n° 5

Problema n° 5) Un auto choca a 60 km/h contra una pared sólida, ¿desde qué altura habría que dejarlo caer para producir el mismo efecto?.

Usar g = 10 m/s².

Desarrollo

Datos:

v_f = 60 km/h
v_f = 16,67 m/s

v₀ = 0 m/s

Ecuaciones:

(1) v_f = v₀ + g.t

(2) y = v₀.t + g.t²/2

(3) v_f² - v₀² = 2.g.h

De la ecuación (3):

v_f²/2.g = h
h = (16,67 m/s)²/[2.(-10 m/s²)]
h = 13,9 m