CAÍDA LIBRE
Se le llama caída libre al movimiento que se debe únicamente a la influencia de la gravedad.
- Todos los cuerpos con este tipo de movimiento tienen una aceleración dirigida hacia abajo cuyo valor depende del lugar en el que se encuentren. En la Tierra este valor es de aproximadamente 9,8 m/s², es decir que los cuerpos dejados en caída libre aumentan su velocidad (hacia abajo) en 9,8 m/s cada segundo .
- En la caída libre no se tiene en cuenta la resistencia del aire.
La aceleración a la que se ve sometido un cuerpo en caída libre es tan importante en la Física que recibe el nombre especial de aceleración de la gravedad y se representa mediante la letra g.
| Lugar | g (m/s²) |
Hemos dicho antes que la aceleración de un cuerpo en caída libre dependía del lugar en el que se encontrara. A la izquierda tienes algunos valores aproximados de g en diferentes lugares de nuestro Sistema Solar.Para hacer más cómodos los cálculos de clase solemos utilizar para la aceleración de la gravedad en la Tierra el valor aproximado de 10 m/s² en lugar de 9,8 m/s², que sería más correcto.
| |
| Mercurio | 2,8 | ||
| Venus | 8,9 | ||
| Tierra | 9,8 | ||
| Marte | 3,7 | ||
| Júpiter | 22,9 | ||
| Saturno | 9,1 | ||
| Urano | 7,8 | ||
| Neptuno | 11,0 | ||
| Luna | 1,6 |
Ecuaciones para la caída libre
e = vo·t + ½·a·t²
vf = vo + a·t
e = ½·a·t²
vf = a·t



Recuerda las ecuaciones generales del movimiento:
vf = vo + a·t
Podemos adaptar estas ecuaciones para el movimiento de caída libre. Si suponemos que dejamos caer un cuerpo (en lugar de lanzarlo), entonces su velocidad inicial será cero y por tanto el primer sumando de cada una de las ecuaciones anteriores también será cero, y podemos eliminarlos:
vf = a·t
Por otro lado, en una caída libre la posición que ocupa el cuerpo en un instante es precisamente su altura h en ese momento.
Como hemos quedado en llamar g a la aceleración que experimenta un cuerpo en caída libre, podemos expresar las ecuaciones así:
Como hemos quedado en llamar g a la aceleración que experimenta un cuerpo en caída libre, podemos expresar las ecuaciones así:
h = ½·g·t²
vf = g·t
vf = g·t
En el gráfico y en la tabla se puede ver la posición de un cuerpo en caída libre a intervalos regulares de 1 segundo.Para realizar los cálculos se ha utilizado el valor g = 10 m/s².
Observa que la distancia recorrida en cada intervalo es cada vez mayor y eso es un signo inequívoco de que la velocidad va aumentando hacia abajo.
Observa que la distancia recorrida en cada intervalo es cada vez mayor y eso es un signo inequívoco de que la velocidad va aumentando hacia abajo.
| tiempo (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| posición (m) | 0 | -5 | -20 | -45 | -80 | -125 | -180 | -245 |
Ahora es un buen momento para repasar las páginas que se refieren a la interpretación de las gráficas e-t y v-t y recordar lo que hemos aprendido sobre ellas.
Ya hemos visto que las gráficas posición-tiempo y velocidad-tiempo pueden proporcionarnos mucha información sobre las características de un movimiento.
Ya hemos visto que las gráficas posición-tiempo y velocidad-tiempo pueden proporcionarnos mucha información sobre las características de un movimiento.
Para la caída libre, la gráfica posición tiempo tiene la siguiente apariencia:

Recuerda que en las gráficas posición-tiempo, una curva indicaba la existencia de aceleración.
La pendiente cada vez más negativa nos indica que la velocidad del cuerpo es cada vez más negativa, es decir cada vez mayor pero dirigida hacia abajo. Esto significa que el movimiento se va haciendo más rápido a medida que transcurre el tiempo.
La pendiente cada vez más negativa nos indica que la velocidad del cuerpo es cada vez más negativa, es decir cada vez mayor pero dirigida hacia abajo. Esto significa que el movimiento se va haciendo más rápido a medida que transcurre el tiempo.

Observa la gráfica v-t de la derecha que corresponde a un movimiento de caída libre.
Su forma recta nos indica que la aceleración es constante, es decir que la variación de la velocidad en intervalos regulares de tiempo es constante.
Su forma recta nos indica que la aceleración es constante, es decir que la variación de la velocidad en intervalos regulares de tiempo es constante.
| tiempo (s) | 0 | 1 | 2 | 3 | 4 | 5 |
| velocidad (m/s) | 0 | -10 | -20 | -30 | -40 | -50 |
La pendiente negativa nos indica que la aceleración es negativa. En la tabla anterior podemos ver que la variación de la velocidad a intervalos de un segundo es siempre la misma (-10 m/s). Esto quiere decir que la aceleración para cualquiera de los intervalos de tiempo es:
g = -10 m/s / 1s = -10 m/s/s = -10 m/s²
¿Una contradicción?
Si has estudiado con atención ésta página, estarás sorprendido porque hemos comenzado diciendo que la aceleración de la gravedad tiene un valor en la Tierra de 10 m/s² y, sin embargo, al realizar el estudio gráfico hemos llegado a la conclusión de que se trataba de un valor negativo: -10 m/s².Recuerda que todas las observaciones que hacemos sobre las características de un movimiento dependen del sistema de referencia elegido (generalmente la Tierra).
En ocasiones nos interesa cambiar nuestro sistema de referencia para expresar los datos con mayor comodidad.
En ocasiones nos interesa cambiar nuestro sistema de referencia para expresar los datos con mayor comodidad.

En el caso de la caída libre, parece lógico situar el sistema de referencia en la posición inicial del cuerpo para medir elalejamiento que experimenta y asignar valores positivos a las distancias recorridas hacia abajo.
| tiempo (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| posición (m) | 0 | 5 | 20 | 45 | 80 | 125 | 180 | 245 |
Esto significa que ahora estamos considerando sentido positivo hacia abajo y sentido negativo hacia arriba, por lo que la gráfica posición-tiempo sería como la anterior.
De la nueva gráfica posición-tiempo deducimos que ahora la velocidad es positiva (hacia abajo) y cada vez mayor porque la pendiente es positiva y cada vez mayor.
El valor que obtenemos ahora para g es +10 m/s², pero no se trata de una contradicción.
Recuerda que hay un convenio para interpretar qué sentido tiene la aceleración:
El siguiente applet simula la caída libre de un cuerpo en diferentes condiciones de gravedad y dibuja las gráficas v-t que corresponden a nuestro nuevo sistema de referencia. Se trata de un cuerpo que lleva enganchada una tira de papel sobre la que un dispositivo realiza marcas a intervalos regulares de tiempo:
De la nueva gráfica posición-tiempo deducimos que ahora la velocidad es positiva (hacia abajo) y cada vez mayor porque la pendiente es positiva y cada vez mayor.
El valor que obtenemos ahora para g es +10 m/s², pero no se trata de una contradicción.
Recuerda que hay un convenio para interpretar qué sentido tiene la aceleración:
Si el móvil está disminuyendo su rapidez (está frenando), entonces su aceleración va en el sentido contrario al movimiento.Si aplicamos este convenio nos damos cuenta de que el sentido de g no ha cambiado: sigue siendo hacia abajo.
Si el móvil aumenta su rapidez, la aceleración tiene el mismo sentido que la velocidad.
El siguiente applet simula la caída libre de un cuerpo en diferentes condiciones de gravedad y dibuja las gráficas v-t que corresponden a nuestro nuevo sistema de referencia. Se trata de un cuerpo que lleva enganchada una tira de papel sobre la que un dispositivo realiza marcas a intervalos regulares de tiempo:
Habrás observado al trabajar con el applet que las gráficas v-t cambian al modificar los valores de g pero no ocurre lo mismo si variamos la masa del cuerpo.
Puede que esto te parezca extraño pero no olvides que sólo llamamos caída libre al movimiento que únicamente está influido por la gravedad.
Si tuviésemos en cuenta la resistencia del aire, sí que tendrían importancia la masa y la forma del cuerpo, pero no se trataría de una caída libre.
Por cierto, ¿sabrías determinar la escala utilizada en el applet para el tiempo y la velocidad?
EJERCICIOS
Veremos y explicaremos varias ejercicios típicos y diferentes de caída libre, pero antes de ver los ejercicios, deberías repasar el tema en este enlace: Caida Libre. Si ya lo sabes todo adelante, vamos a ver los ejercicios. No obstante aquí tienes las 3 fórmulas principales:
Primera: V = Vo +- gt
Segunda: Y = Vo t + Yo - 0.5 gt² Recuerda 1/2 = 0.5 y la fórmula se verá:
Y = Vo . t + 1/2 gt², pero es la misma.
Tercera: V² = Vo² - 2g( Y – Yo) otra forma de verla sería poniendo las velocidades a un lado de la ecuación:
V² - Vo² = - 2g( Y – Yo), pero es la misma fórmula.
Donde V es velocidad final, g la gravedad (en la tierra 9,8m/s, se puede aproximar a 10), Vo velocidad inicial, Vm velocidad media, t es el tiempo, la Y es la altura final (si cae en el suelo será cero), la Yo es la altura inicial desde donde se suelta el objeto. Ojo en algunos libros veremos como a las Y se les llama h o altura.
Ojo si el objeto lo soltamos desde una altura, su Vo = 0 (parte su descenso sin velocidad) y si la altura final es el suelo entonces Y = 0.
Primera: V = Vo +- gt
Segunda: Y = Vo t + Yo - 0.5 gt² Recuerda 1/2 = 0.5 y la fórmula se verá:
Y = Vo . t + 1/2 gt², pero es la misma.
Tercera: V² = Vo² - 2g( Y – Yo) otra forma de verla sería poniendo las velocidades a un lado de la ecuación:
V² - Vo² = - 2g( Y – Yo), pero es la misma fórmula.
Donde V es velocidad final, g la gravedad (en la tierra 9,8m/s, se puede aproximar a 10), Vo velocidad inicial, Vm velocidad media, t es el tiempo, la Y es la altura final (si cae en el suelo será cero), la Yo es la altura inicial desde donde se suelta el objeto. Ojo en algunos libros veremos como a las Y se les llama h o altura.
Ojo si el objeto lo soltamos desde una altura, su Vo = 0 (parte su descenso sin velocidad) y si la altura final es el suelo entonces Y = 0.
Ejercicio 1. Un cuerpo cae libremente desde el reposo durante 6 segundos hasta llegar al suelo. Calcular la distancia que ha recorrido, o lo que es lo mismo, la altura desde donde se soltó.
Datos que tenemos:
Velocidad inicial ………. Vo = 0 (la soltamos y parte de velocidad cero)
Tiempo de caída …….…... t = 6 s
Aceleración de caída …... g = 10 m/s2 (aproximamos en lugar de 9,8)
Altura final será el suelo = 0 (Nota: aunque no fuera el suelo en caída libre la altura final siempre = 0)
Parte de una altura inicial Yo = ??? es la que nos piden, también podemos llamarla altura o "h".
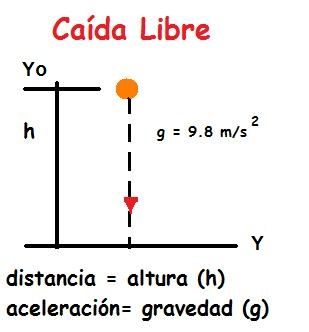
Aplicaremos la segunda fórmula :
Y = vo t + Yo - 0.5 gt² donde Yo será la altura inicial o altura desde la que cae (h).
poniendo valores en la fórmula :
0 = Yo -0.5 ( 10 x 6²) ==> despejando Yo
-Yo = - 180 Los signos menos se nos marchan en los dos miembros de la ecuación y quedarán positivos.
Yo = 180m Resuelto h = 180 metros
Datos que tenemos:
Velocidad inicial ………. Vo = 0 (la soltamos y parte de velocidad cero)
Tiempo de caída …….…... t = 6 s
Aceleración de caída …... g = 10 m/s2 (aproximamos en lugar de 9,8)
Altura final será el suelo = 0 (Nota: aunque no fuera el suelo en caída libre la altura final siempre = 0)
Parte de una altura inicial Yo = ??? es la que nos piden, también podemos llamarla altura o "h".

Aplicaremos la segunda fórmula :
Y = vo t + Yo - 0.5 gt² donde Yo será la altura inicial o altura desde la que cae (h).
poniendo valores en la fórmula :
0 = Yo -0.5 ( 10 x 6²) ==> despejando Yo
-Yo = - 180 Los signos menos se nos marchan en los dos miembros de la ecuación y quedarán positivos.
Yo = 180m Resuelto h = 180 metros
Ejercicio 2. Un tornillo cae accidentalmente desde la parte superior de un edificio. 4 segundos después está golpeando el suelo. ¿Cual será la altura del edificio?.
Datos iniciales:
Velocidad inicial ................... Vo = 0
tiempo de caída ...................... t = 4s
aceleración de caída ............... g = 10 m/s2
altura de caída (edificio ) .......... h = ? (en la fórmula será Yo)
Aplicamos la segundo fórmula Y = vo t + Yo - 0.5 gt² o lo que es lo mismo Y = Vo . t - 1/2 gt². En nuestro caso tenemos qué:
0 = Yo - 1/2 ( 10 x 4²) = => 0 = Yo - 80 ;despejando Yo
Yo = 80 metros Resuelto
Ejercicio 3. Desde el techo de un edificio se deja caer una piedra hacia abajo y se oye el ruido del impacto contra el suelo 3 segundos después. Sin tomar en cuenta la resistencia del aire, ni el tiempo que tardó el sonido en llegar al oído, calcula:
a) La altura del edificio.
b) La velocidad de la piedra al llegar al suelo.
Considerar g = 10 m/s²
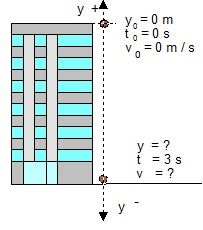
Primero calculamos el apartado b). Aplicamos la primera fórmula: V = Vo +- gt, para calcular la velocidad a la que llega al suelo, sabiendo que Vo = cero y que el signo es + por ir cada vez más rápido la piedra. La fórmula quedará V = gt
V = 10 x 3 = 30 m/s Resuelto.
Ahora para el apartado a) aplicamos la segundo fórmula sabiendo que Y (final) es cero por que acaba en el suelo y la Vo sigue siendo cero también. La fórmula quedará:
Y = Yo - 0.5 gt²
0 = Yo - (0.5 x 10 x 3²) = Yo - 35 Despejando Yo tenemos:
Yo = 45 metros Resuelto.
Datos iniciales:
Velocidad inicial ................... Vo = 0
tiempo de caída ...................... t = 4s
aceleración de caída ............... g = 10 m/s2
altura de caída (edificio ) .......... h = ? (en la fórmula será Yo)
Aplicamos la segundo fórmula Y = vo t + Yo - 0.5 gt² o lo que es lo mismo Y = Vo . t - 1/2 gt². En nuestro caso tenemos qué:
0 = Yo - 1/2 ( 10 x 4²) = => 0 = Yo - 80 ;despejando Yo
Yo = 80 metros Resuelto
Ejercicio 3. Desde el techo de un edificio se deja caer una piedra hacia abajo y se oye el ruido del impacto contra el suelo 3 segundos después. Sin tomar en cuenta la resistencia del aire, ni el tiempo que tardó el sonido en llegar al oído, calcula:
a) La altura del edificio.
b) La velocidad de la piedra al llegar al suelo.
Considerar g = 10 m/s²

Primero calculamos el apartado b). Aplicamos la primera fórmula: V = Vo +- gt, para calcular la velocidad a la que llega al suelo, sabiendo que Vo = cero y que el signo es + por ir cada vez más rápido la piedra. La fórmula quedará V = gt
V = 10 x 3 = 30 m/s Resuelto.
Ahora para el apartado a) aplicamos la segundo fórmula sabiendo que Y (final) es cero por que acaba en el suelo y la Vo sigue siendo cero también. La fórmula quedará:
Y = Yo - 0.5 gt²
0 = Yo - (0.5 x 10 x 3²) = Yo - 35 Despejando Yo tenemos:
Yo = 45 metros Resuelto.
Ejercicio 4. ¿Con qué velocidad se debe lanzar hacia arriba, una piedra, para que logre una altura máxima de 3.2 m?
Datos iniciales:
Velocidad inicial ............. Vo = ?
Velocidad final ................ Vf = 0 (cuando llega a la altura máxima y se para)
altura máxima alcanzada .. Y = 3,2 m
altura inicial Yo = 0 (se lanza desde el suelo)
aceleración actuante ........ g = 10 m/s2
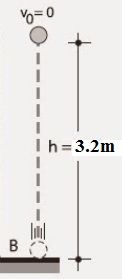
Aplicaremos la tercera fórmula ya que no nos dan el tiempo:
Vf² = Vo² - 2g( Y – Yo)
0 = Vo² - 2 x 10 ( 3,2 - 0) =
0 = Vo² - 64 despejamos la velocidad inicial del lanzamiento Vo ===>
Vo = √ 64 m/s = 8m/s Resuelto
Datos iniciales:
Velocidad inicial ............. Vo = ?
Velocidad final ................ Vf = 0 (cuando llega a la altura máxima y se para)
altura máxima alcanzada .. Y = 3,2 m
altura inicial Yo = 0 (se lanza desde el suelo)
aceleración actuante ........ g = 10 m/s2

Aplicaremos la tercera fórmula ya que no nos dan el tiempo:
Vf² = Vo² - 2g( Y – Yo)
0 = Vo² - 2 x 10 ( 3,2 - 0) =
0 = Vo² - 64 despejamos la velocidad inicial del lanzamiento Vo ===>
Vo = √ 64 m/s = 8m/s Resuelto
Ejercicio 5. Hallar la velocidad con que fue lanzado un proyectil hacia arriba si ésta se reduce a la tercera parte cuando ha subido 40 m. (g = 10 m/s2)
Datos iniciales
La velocidad inicial es 3 veces mayor que la inicial, ya que se redujo 3 veces. La Yo se considera el suelo luego Yo = 0
Velocidad final .............. Vf = Vo/3 de aquí despejamos Vo y tenemos ==>
Velocidad inicial..............Vo = Vf x 3
altura ............................. h = 40m
aceleración de subida ...... g = -- 10 m/s2
Aplicamos la tercera fórmula V² - Vo² = - 2g( Y – Yo) y donde pone Vo ponemos = V x 3 ( 3 veces mayor como nos dice el problema)
V² - Vo² = - 2g( Y – Yo) ==> V² - (3V)² = - 2 x 10( 40 – 0) quedará:
V² - 9V² = - 800
OJO (3V)² son 3V² x 3V² = 9V² (OJO NO puedes hacer V² - 3Vo² = 2 V² estaría mal)
-8V² = -800 ==> Podemos cambiar los signos menos por más ya que están a los dos lados de la ecuación.
V² = 800/8 = 100 Luego...
V = √100 = 10 m/s Resuelto
Datos iniciales
La velocidad inicial es 3 veces mayor que la inicial, ya que se redujo 3 veces. La Yo se considera el suelo luego Yo = 0
Velocidad final .............. Vf = Vo/3 de aquí despejamos Vo y tenemos ==>
Velocidad inicial..............Vo = Vf x 3
altura ............................. h = 40m
aceleración de subida ...... g = -- 10 m/s2
Aplicamos la tercera fórmula V² - Vo² = - 2g( Y – Yo) y donde pone Vo ponemos = V x 3 ( 3 veces mayor como nos dice el problema)
V² - Vo² = - 2g( Y – Yo) ==> V² - (3V)² = - 2 x 10( 40 – 0) quedará:
V² - 9V² = - 800
OJO (3V)² son 3V² x 3V² = 9V² (OJO NO puedes hacer V² - 3Vo² = 2 V² estaría mal)
-8V² = -800 ==> Podemos cambiar los signos menos por más ya que están a los dos lados de la ecuación.
V² = 800/8 = 100 Luego...
V = √100 = 10 m/s Resuelto
Ejercicio 6. Hallar la aceleración de la gravedad en un planeta conociéndose que en éste, cuando un cuerpo es soltado desde una altura de 4m, tarda 1s para golpear en el suelo.
Datos iniciales:
En este caso nos piden la gravedad "g" del planeta.
Velocidad inicial ......... Vo = 0
altura de caída ............. h = 4m
aceleración de caída...... g = ?
tiempo de caída ............ t = 1s
Aplicamos la segundo fórmula y despejaremos g.
Y = Vo t + Yo - 0.5 gt² ===> Ponemos datos:
4 = 0 + 1/2 x g x 1² ==>
4 = 1/2g ==>
despejando g:
g = 4 x 2 = 8 m/s² Resuelto.
Datos iniciales:
En este caso nos piden la gravedad "g" del planeta.
Velocidad inicial ......... Vo = 0
altura de caída ............. h = 4m
aceleración de caída...... g = ?
tiempo de caída ............ t = 1s
Aplicamos la segundo fórmula y despejaremos g.
Y = Vo t + Yo - 0.5 gt² ===> Ponemos datos:
4 = 0 + 1/2 x g x 1² ==>
4 = 1/2g ==>
despejando g:
g = 4 x 2 = 8 m/s² Resuelto.

No hay comentarios:
Publicar un comentario