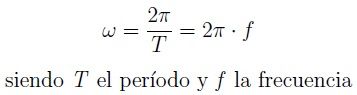MCUV

Movimiento circular uniformemente variado

En MCUV el móvil se desplaza sobre una circunferencia variando el módulo tanto de su velocidad angular como tangencial continuamente. Existen una aceleración tangencial y una aceleración angular, que modifican a las velocidades correspondientes.

Un movimiento circular es “variado” cuando varía su velocidad angular.

FÓRMULAS

EJERCICIOS

Ejercicios sobre el movimiento circular variado (acelerado)

Ejercicio 1)

Un automóvil, cuyo velocímetro indica en todo instante 72 km/h, recorre el perímetro de una pista circular en un minuto. Determinar el radio de la misma. Si el automóvil tiene una aceleración en algún instante, determinar su módulo, dirección y sentido.

Si la pista es circular, la velocidad que tiene el auto es la velocidad tangencial. Si da una vuelta a la pista en un minuto, significa que su periodo (T) es de un minuto.

Ahora, como  , entonces:
 velocidad  angular .

Por otro lado, la velocidad tangencial es 20 m/s (72 km/h), reemplazando en la fórmula:

Tenemos

Calculamos r:

R = 192 m Radio de la pista

Ahora, aunque su velocidad  (rapidez) sea constante, igual tiene aceleración centrípeta, cuyo módulo es

Aceleración centrípeta, dirigida hacia el centro de la pista.

MCU

El movimiento circular uniforme (MCU) es el movimiento que describe una partícula cuando da vueltas sobre un eje estando siempre a la misma distancia (r) del mismo y desplazándose a una velocidadconstante.

Se define como movimiento circular aquél cuya trayectoria es una circunferencia.

El movimiento circular del piñón se transforma en movimiento lineal en la cremallera.

El movimiento circular, llamado también curvilíneo, es otro tipo de movimiento sencillo.

Estamos rodeados por objetos que describen movimientos circulares:  un disco compacto durante su reproducción en el equipo de música, las manecillas de un reloj o las ruedas de una motocicleta son ejemplos de movimientos circulares; es decir, de cuerpos que se mueven describiendo una circunferencia.

A veces el movimiento circular no es completo: cuando un coche o cualquier otro vehículo toma una curva realiza un movimiento circular, aunque nunca gira los 360º de la circunferencia.

La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).

Ejemplos de cosas que se mueven con movimiento circular uniforme hay muchos:

La tierra es uno de ellos. Siempre da una vuelta sobre su eje cada 24 horas. También gira alrededor del sol y da una vuelta cada 365 días. Un ventilador, un lavarropas o los viejos tocadiscos, la rueda de un auto que viaja con velocidad constante, son otros tantos ejemplos.

Pero no debemos olvidar que también hay objetos que giran con movimiento circular variado, ya sea acelerado o decelerado.

El movimiento circular en magnitudes angulares

La descripción de un movimiento circular puede hacerse bien en función de magnitudes lineales ignorando la forma de la trayectoria (y tendremos velocidad y aceleración tangenciales), o bien en función de magnitudes angulares (y tendremos velocidad y aceleración angulares).  Ambas descripciones están relacionadas entre sí mediante el valor del radio de la circunferencia trayectoria.

Al trabajar con magnitudes angulares es imprescindible entender lo relativo a una unidad de medida angular conocida como radián.

Ángulo θ con centro en C.

El radián

Si tenemos un ángulo cualquiera y queremos saber cuánto mide, tomamos un transportador y lo medimos. Esto nos da el ángulo medido en grados. Este método viene de dividir la circunferencia en 360º, y se denomina sexagesimal.

(Para usar la calculadora en grados hay que ponerla en DEG, Degrees, que quiere decir grados en inglés).

El sistema de grados sexagesimales es una manera de medir ángulos, pero hay otros métodos, y uno de ellos es usando radianes.

Ahora veamos el asunto de medir los ángulos pero en radianes.

Para medir un ángulo en radianes se mide el largo del arco (s) abarcado por el ángulo θ de la figura a la izquierda. Esto se puede hacer con un centímetro, con un hilito o con lo que sea. También se mide el radio del círculo.

Para obtener el valor del ángulo (θ) en radianes  usamos la fórmula:

 y tenemos el ángulo medido en radianes

Hacer la división del arco sobre radio significa ver cuántas veces entra el radio en el arco. Como el radio y el arco deben medirse en la misma unidad,  el radián resulta ser un número sin unidades.

Esto significa que el valor del ángulo en radianes solo me indica cuántas veces entra el radio en el arco. Por ejemplo, si el ángulo θ mide 3 radianes, eso significa que el radio entra 3 veces en el arco abarcado por ese ángulo.

Su quisiéramos calcular o conocer al valor del arco, hacemos:

¿Cuántas veces entra el radio en el arco marcado?

¿A cuántos grados equivale un radián?

Pero el valor de un ángulo en radianes se puede expresar (convertir) en grados. En una circunferencia entera (360º) el arco entero es el perímetro, que es igual a 2 Pi por radio . Así, a partir de la fórmula
 es que 360° equivalen a:

Un ángulo de un radián equivale a un ángulo de 57,3º.

Para usar la calculadora en radianes hay que ponerla en "RAD" 

FÓRMULAS

Velocidad angular

En el MCU, la velocidad angular se puede calcular a partir del período o la frecuencia, ya que el períodoy la frecuencia son constantes.

Otra forma de determinar la velocidad angular es:

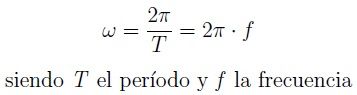
Las unidades en las que se mide la velocidad angular ω es en radianes/seg, o simplemente en s^-1.

La velocidad angular en el MCU es constante.

Velocidad tangencial

La velocidad tangencial es igual a la velocidad angular por el radio.

La velocidad tangencial, al igual que la velocidad angular, en el MCU es constante.

Aceleración centrípeta

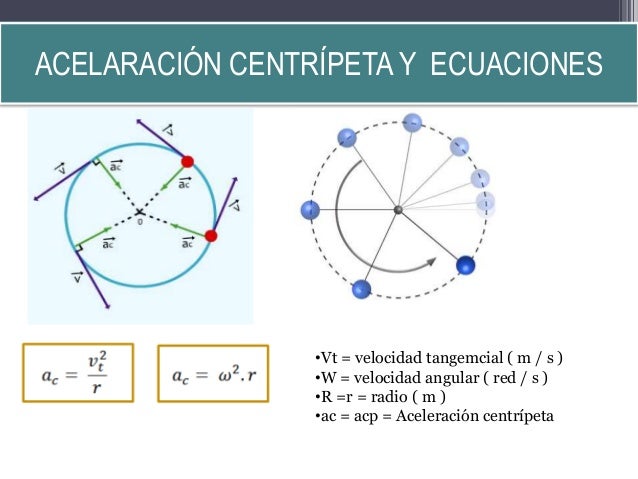
A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de lavelocidad se mantiene constante, el vector cambia constantemente de dirección. Ésta se calcula como:

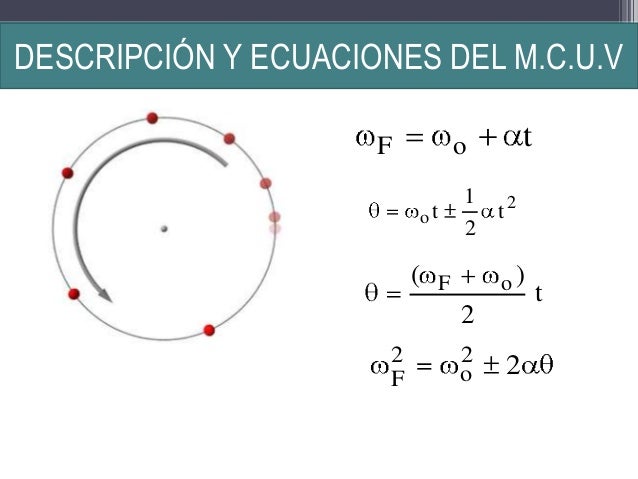
Aceleración angular y tangencial

En el movimiento circular uniforme (MCU), tanto la aceleración angular como la aceleración tangencialesson cero.

Período

La velocidad angular en el MCU es constante, por lo que el período también será constante e irá definido por la fórmula siguiente:

Frecuencia

La frecuencia es constante al ser constante la velocidad angular y el período:

EJERCICIOS

Una rueda gira a una velocidad constante de 120 revoluciones por minuto (r.p.m.). Hallar:

1. La frecuencia en ciclos/segundo.
2. La velocidad angular en radianes/segundo.
3. La velocidad tangencial en un punto de la rueda situado a 15 cm. del eje.
4. Las aceleraciones tangenciales y centrípetas en el punto citado.

Solución:

1. La frecuencia en ciclos/segundo se calcula dividiendo las r.p.m. entre los 60 segundos que tiene un minuto:
   
   
2. La velocidad angular (ω):
   
   
3. La velocidad tangencial en un punto de la rueda situado a 15 cm del eje, el radio de rotación será de r=15 cm, por lo tanto:
   
   
4. La aceleración tangencial es 0:
   
   
   La aceleración centrípeta en el punto citado es:
   
   

Ejercicios sobre movimiento circular uniforme

Ejercicio 1)

Un móvil con trayectoria circular recorrió 820° ¿Cuántos radianes son?

Desarrollo

Sabemos que 1 rad = 57,3°

Entonces 

Ejercicio 2)

Como en un tractor, la rueda delantera es más chica.

Un tractor tiene una rueda delantera de 30 cm de radio, mientras que el radio de la trasera es de 1 m. ¿Cuántas vueltas habrá dado la rueda trasera cuando la delantera ha completado 15 vueltas?

Desarrollo:

En este ejercicio la longitud (distancia, espacio) que recorre cada rueda en una vuelta corresponde al perímetro de cada una (perímetro del círculo), cuya fórmula es , entonces:

Entonces, si en una vuelta la rueda delantera recorre 1,884 metro, en 15 vueltas recorrerá: 15 • 1,884 m = 28,26 m

¿Cuantas veces la rueda trasera ha tenido que girar (dar una vuelta) para recorrer esa distancia de 28,26 m?

Dividimos  esa distancia por la distancia recorrida en una vuelta por la rueda trasera:

28,26 m : 6,28 m = 4,5 vueltas.

Por lo tanto, la rueda trasera ha tenido que dar cuatro vueltas y media para recorrer la misma distancia que la delantera ha recorrido en 15 vueltas.

TIRO HORIZONTAL

Lanzamiento Horizontal

El lanzamiento horizontal es un tipo de movimiento que explica la interacción que tiene un "móvil" al estar en movimiento con una serie de factores físicos. Este movil durante su trayectoria tiene una serie de características específicas que lo diferencia de otro tipo de movimiento. Dichas características son:

* Tiene una relación directa con la "caída libre", la cual según Brett C., E., Suárez, W. A. (2012) "es el movimiento, en dirección vertical, con aceleración constante realizado por un cuerpo cuando se deje caer en el vacío".

* Este tipo de lanzamiento combina dos tipos de movimientos: el vertical (producido por la caída libre) y el vertical (definido como un Movimiento Rectilíneo Uniforme).

* Ya que tiene dos movimientos, uno que atrae (la gravedad), y otro que hace mover al móvil hacia un lado “horizontal” (MRU), tenemos que la trayectoria es una semiparábola.

Lanzamiento Horizontal

El movimiento de un proyectil en lanzamiento horizontal es un caso especial del movimiento en dos dimensiones.

De este modo, el lanzamiento horizontal es un movimiento que consiste en un movimiento de un cuerpo que se lanza horizontalmente con una velocidad en el eje X, vox , desde una cierta altura, y, sobre la superficie de la Tierra este movimiento es el resultado de dos movimientos perpendiculares entre si, teniendo las siguientes características:Cuando este tipo de movimiento se analiza como dos movimientos perpendiculares entre sí, el desplazamiento en cada dirección depende de la velocidad y la aceleración en esa dirección.

• Es un movimiento rectilíneo y uniforme en el eje X, con velocidad Vo.
• Es un movimiento rectilíneo uniformemente acelerado según el eje Y, con velocidad nula y aceleración-g.
• La trayectoria es curva y la forma de la curva descrita es abierta, simétrica respecto a un eje (eje Y) y con un solo foco, es decir una parábola.

Para analizar el lanzamiento horizontal y del cuerpo en caída libre, debe emplearse un sistema de coordenadas x y y perpendiculares, cuyo origen se encuentra ubicado en el punto de salida del proyectil. En este sentido, debe considerarse lo siguiente:

• Si V0 es la magnitud de la velocidad inicial con la cual es lanzado el proyectil, su movimiento horizontal tendrá una velocidad constante de magnitud igual a V0, ya que en esta dirección no actúa fuerza alguna;
• En cambio, en la dirección vertical siempre actúa una fuerza constante sobre el proyectil, que es la fuerza de atracción gravitacional de la tierra. Así, en la dirección vertical, el movimiento es uniformemente acelerado con una aceleración de magnitud – g, donde g es el valor numérico de la aceleración de la gravedad.

Así pues, en el movimiento horizontal las coordenadas de la posición, x e y:

Componente horizontal: x= V0 t

Componente vertical: y = y0 – ½ gt2

Ecuación de la posición: r = v0 t i+(y0 – ½ gt2)j .

Igualmente, combinando ambos movimientos se podrá conocer la velocidad del objeto en cualquier instante:

Velocidad de avance horizontal: Vx = Vox

Velocidad de caída vertical: Vy = -gt

Ecuación de la velocidad: V = V0x – gt

Compártelo:

* Sí presenta un movimiento de caída libre, tenemos que la aceleración es la gravedad, la cual es: 9.8 m/s².

* La Velocidad Inicial tiene solo componente horizontal, ya que la misma es accionada en sentido “horizontal” (valga la redundancia).

* La Velocidad dependerá de la altura del lanzamiento.

FÓRMULAS

La velocidad es aquella “distancia” que recorre el móvil en cierta cantidad de tiempo. Básicamente se calcula dividiendo la distancia recorrida entre el tiempo en que duro su trayecto. En este caso, tenemos dos tipos de velocidades en este lanzamiento, la velocidad “Vx” y la velocidad “Vy”.

La velocidad en “x” (Vx) se calcula de la siguiente manera:

Vo = Vx =  x / t    (x = distancia recorrida; t = tiempo)

La velocidad en “y” (Vy) se calcula de la siguiente manera:

Vy =  g t              (g = gravedad; t = tiempo)

La velocidad cuadrar en “y” (Vy²) se calcula de la siguiente manera:

Vy² =  2 g t

El componente “y” o altura se calcula de la siguiente manera:

Y = 0.5 g t²

Velocidad a cualquier instante

Dirección de la velocidad:

 

Tiempo de vuelo:

Alcance horizontal:

EJERCICIOS

Una pelota de tenis situada a 2 metros de altura es golpeada por un jugador con su raqueta. La pelota sale despedida horizontalmente con una velocidad de 30 m/s. Responde a las siguientes preguntas:

a) ¿Cuanto tiempo tarda la pelota en llegar al suelo?
b) ¿Qué ángulo forma el vector velocidad con el eje X en el momento que alcanza el suelo?
c) Si antes del golpe, la pelota se encuentra a 5 metros de la red ¿A qué altura pasa la pelota sobre la red?

uestión a)

La pelota llegará al suelo cuando su posición Y sea 0 (y=0). Según las ecuaciones del lanzamiento horizontal:

y=H−12⋅g⋅t2⇒0=2 m−0.5⋅9.8 ms2/⋅t2⇒t=0.63 s

Cuestión b)

Para calcular el ángulo que forma el vector velocidad con el eje X, utilizaremos la siguiente expresión:

tan(α)=vyvx

Para resolverlo calcularemos vx e vy:

vx=v0=30 ms/vy=−g⋅t ⇒vy=−9.8 ms2/⋅0.63s=−6.17 ms/

Una vez que ya tenemos los datos de la velocidad, podemos obtener el ángulo:

tan(α)=−6.17 ms/30 ms/⇒tan(α)=−0.205 ⇒α=−11.62°

Cuestión c)

Para calcular la altura a la que pasa la pelota sobre la red, en primer lugar deberemos saber en que instante de tiempo pasa por encima de ella. Para ello, sabiendo que la pelota se encuentra a 5 m y que avanza con un m.r.u. a 30m/s:

x=v0⋅t ⇒5 m=30 ms/⋅t ⇒t=0.17 s

En ese instante de tiempo la pelota se encuentra justo sobre la red, basta con calcular su posición y habremos resuelto el problema:

y=H−12⋅g⋅t2⇒2−0.5⋅9.8 ms2/⋅(0.17 s)2⇒y=1.86 m